BET方程适用于微孔吸附剂吗？

微孔通常呈现 IUPAC 分类中的 I 型吸附等温线，和 Langmuir 等温线相似，因此看起来很自然也很简单：直接对这些等温线使用 Langmuir 方程即可。

然而，这其实并不合适，原因如下：

1.Langmuir 方程明确建立在“化学吸附 + 单层吸附 + 与气相自由接触"的特定条件下；而微孔吸附完全不同：

• 吸附不一定局限于表面位点（可能发生孔填充）；

• 大多数吸附相并不与气相直接接触。

2.如果材料是纯微孔，其等温线是完美的 I 型，平台区就直接给出微孔容量，无需额外假设，因此也无需使用 Langmuir 方程。

3.微孔材料的吸附等温线通常是复合型，如：

• I + II 型（分别由微孔与外表面贡献）；

• I + IV 型（分别由微孔与中孔贡献）。

而 Langmuir 理论只适用于单一机理，因此不能用于复合等温线。结果是：计算得到的“Langmuir 单层容量"并不会在拟合压力区间内达到饱和，而是在更高压力下才能完成，显示其理论不一致性。

因此，我们得出结论：诠释微孔材料的吸附等温线需要比 Langmuir 方程更恰当的方法。那么 BET 方程是否是一个好的选择？

BET 方法本质上是一种数学分析技术，用于根据等温线推算“单层容量"和比表面积。其理论依赖多个假设，主要包括（简述）：

然而，对于微孔（以及一般多孔）材料：

因此，有必要重新讨论 BET 方法在微孔材料中的意义。

即使实验精度已不再是问题（现代仪器精确且脱气稳定），

同一可靠等温线仍可能给出多个 BET 单层容量值。

原因是 BET 方程须拟合 BET 图线的线性区，但图中的多个区段可能看起来都很线性，选择具有主观性。

Brunauer 曾建议统一使用 0.05–0.35 的相对压力区间，这对 II 型或 IV 型（无强吸附或无微孔）较合适，但对于含微孔材料，这一范围远超实际线性区范围。

例如文中图 1（Ar/13X @87K）中：

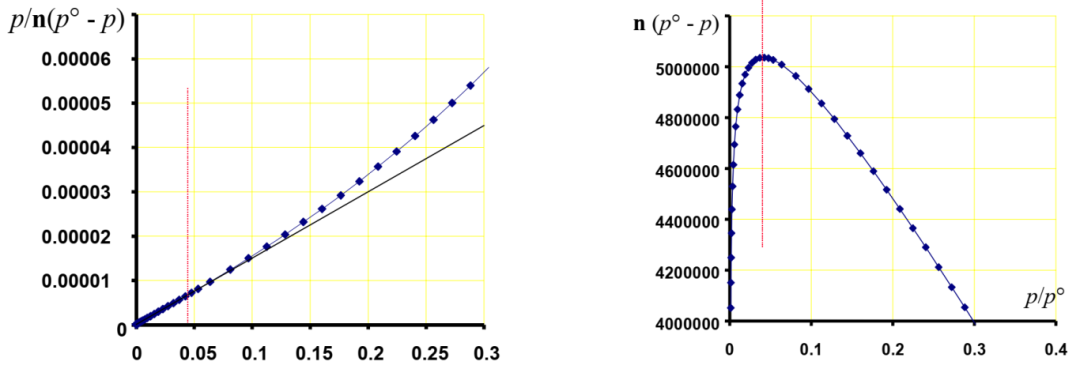
图一：氩气在13X沸石上（87K下）的BET作图；n^a（ p^o-p）随p/p^o的变化关系图

不同选择的线性区产生的单层容量差异达 30%。

因此需额外的“客观选择"标准：

BET 图线区间选择的两个客观标准

1.截距必须为正（C>0），否则无物理意义。

→可排除部分区间。

2.nₐ(p°−p) 必须随 p/p° 单调上升，否则区间过宽。

→进一步排除更高压力的区间。

应用这两条后，得到唯一合理的线性段，从而得到更一致的 BET 单层容量。

此外，我们还始终应用以下两个额外自洽性检查，并且从未见过它们失败：

1. 将计算得到的 BET 单层容量标示在吸附等温线上，其对应的相对压力 p/p°ₘ 应位于用于 BET 拟合的压力区间之内.

2. 另一种方式是：利用计算得到的 C 值，在 BET 方程中设定 nₐ = nₐₘ，重新计算 p/p°ₘ

重新计算的 p/p°ₘ 应与实验等温线上阅读得到的值相差不超过约 10%。

量热实验证明：

• 在能量均一的表面（如石墨化碳）上，分子–分子相互作用不可忽略;

• 在一般的氧化物表面上，表面能量常具异质性;

但二者部分抵消，使得 BET 假设在实践中“勉强可用"。

在微孔材料中，量热曲线显示：BET 所得“单层容量"恰对应吸附质与表面之间最强能量作用的区段。

这是关键观察。

文中展示了 4 个示例（Silicalite、ZSM-48、微孔炭、微孔硅）:

例 1：77 K 下甲烷在 Silicalite 上的吸附

如后续图形一样，吸附等温线从左下角开始，其初始陡峭部分与纵轴几乎重合。量热曲线从右下角开始，使用同一纵坐标（对应吸附量），而吸附微分焓标注在图上方。需要首先注意的是：在大部分吸附范围内，吸附焓始终维持在一个高且恒定的值：–17 kJ·mol⁻¹，超过液化焓的两倍。虽然数值恒定，但并不支持 BET 假设中的“第一层吸附能量恒定"，因为 Silicalite 是典型的微孔材料，这里观察到的并不是单分子层的铺展，而是微孔容积的填充。由于大部分孔填充（最高至约 4 mmol·g⁻¹）都发生在低于 10⁻² mbar 的压力下，因此只有直接量热法能给出可靠的吸附焓；而等量线法（isosteric method）在此完全不可靠，因为它受压力误差或微量杂质（如 N₂ 或 O₂）的影响极大。我们还注意到，这两条曲线呈现出显著的镜像关系：在 I 型等温线进入平台（微孔填满）后，吸附焓立即下降。使用前文的 BET 判据得到的表观单层容量为 4.2 mmol·g⁻¹，对应等温线的“拐点（knee）"。量热曲线显示，这个表观 BET 单层容量恰好对应吸附质的最强吸附部分。

例 2：77 K 下甲烷在微米级 ZSM-48 上的吸附

ZSM-48 的外表面积约 50 m²·g⁻¹，孔径 5–6 nm。尽管其孔道仍高度有序，但无论是等温线还是量热曲线，都与上面例子非常不同。吸附等温线呈明显的复合类型（I 型 + II 型），可归因于显著的外表面积——外表面的吸附效应与微孔吸附共同作用形成了此种等温线形态。

量热曲线也比前一个例子更为复杂，因为现在可以清楚地区分出三个阶段：

• 步骤 1（右下角的初始陡直部分）：对应微孔填充，其吸附焓与在 Silicalite 上的情况一样高。陡直段前的小“尾巴"说明存在少量缺陷或异质性，这些在 Silicalite 中并未观察到（很可能也并不存在）。

• 步骤 2（从约 12 kJ·mol⁻¹ 开始，持续下降并接近液化焓）：对应外表面上统计单层的形成（即第一层和其上层同时形成）。

• 步骤 3（最终的陡直部分，吸附焓为液化焓水平）：对应上层吸附（即“多层吸附"）的形成。

在这里，表观 BET 单层容量（1.9 mmol·g⁻¹）再次恰好对应吸附质的最强吸附部分。

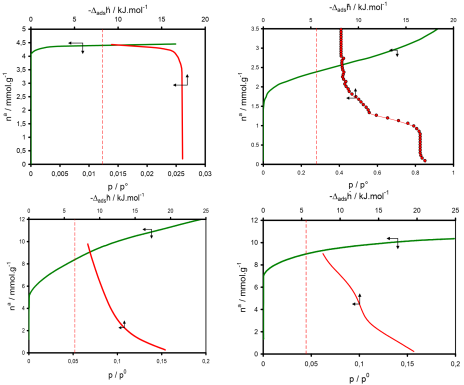
图二： 77 K 下四种体系的吸附等温线（绿色，左）与量热曲线（红色，右）：甲烷在 Silicalite 上（左上）、甲烷在沸石 ZSM-48 上（右上）、氮气在微孔碳上（左下）以及氩气在微孔硅胶（Davison 950）（右下）上的吸附行为。

例 3：77 K 下氮气在微孔碳上的吸附

氮气在活性炭（charcoal 26）上的吸附呈现出与上例类似的几个特征：

• 等温线呈 I 型 + II 型复合；

• 量热曲线至少包含两个明显阶段。

但不同之处在于：初始吸附焓的下降更陡峭、范围更宽，这归因于活性炭的高异质性，同时氮气分子具有永久四极矩，因此比甲烷分子对表面异质性更敏感。

例 4：77 K 下氩气在微孔硅胶上的吸附

等温线再次呈复合类型，而吸附焓随吸附量稳步下降，说明材料包含宽分布的微孔，其中一部分是超微孔（与活性炭类似）。

众所周知，当材料中存在微孔时，“BET 单层容量"这一概念本身并不充分，也没有明确的物理或理论意义，因为微孔中不存在真正的单层结构。

然而，如果我们希望在微孔材料中依然保留 BET 方程的优势（前文所述），就必须引入另一个概念。

幸运的是，量热实验提供了一个启发： “BET 单层容量"在物理上对应着能量上被强烈吸附（或强烈滞留）的吸附质部分。因此，该由 BET 方程给出的量，可以更恰当地称为“BET强滞留容量（BET strong retention capacity）"。

这一容量包含两部分：

1.微孔容量；

2.非微孔表面上的单层容量

第二部分对应外表面积（external surface area），可通过α_s或 t方法轻松确定，并不需要依赖等温线的超低压部分。

其中：若希望对微孔进行更精细的分析，并且拥有低压段数据，则优先使用α_s方法；

若只需获得可靠的外表面积，则t方法更简单，只需在软件中加入适当的多层吸附方程，例如 Harkins–Jura t 曲线方程。

因此，推荐的计算流程如下：

1.利用 BET 方程与第 3 节给出的判据，计算BET强滞留容量

2.利用α_s或t方法计算外表面积a_ext，并得到对应的外表面单层容量

3.计算微孔容量，即：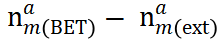

值得指出的是：微孔容量（针对特定吸附质）具有明确物理意义，远比“微孔体积"可靠；后者依赖于微孔内吸附质的未知堆积方式，因此常常不准确。

4.针对同一吸附质，通过最终平台（通常在 p/p° ≥ 0.9）上的饱和吸附量确定“饱和容量"（saturation capacity）

上述四个量值可以以软件方式自动计算

无论是什么吸附剂，若存在微孔，它们均具有明确意义；若不存在微孔，则“微孔容量"自然应接近零，仅在这种情况下，“BET 单层容量"这一概念才可以毫无歧义地恢复使用。

1.BET 方法并非为微孔吸附剂设计，因此不应对含微孔材料盲目使用（Langmuir 方程更不应如此）

2.除了 BET 图的线性判据之外，还需要额外两个判据（尤其在存在微孔时）以发挥 BET 方程的特定优势，即获得单一且可重现的“单层容量"值

3.微孔吸附剂的量热数据表明，按上述判据算得的 BET 单层容量主要对应与表面存在强能量相互作用的吸附量

4.对于含微孔的吸附剂，“BET单层容量"概念是不恰当的，可替换为“BET强滞留容量"。该量包含微孔吸附与外表面的统计单层吸附两部分

5.与其使用“不够可靠的 BET 表面积（对微孔不适用）"或“微孔体积（受未知堆积结构影响）"，更安全、物理意义更明确的量应是：

* BET强滞留容量

* 外表面积

* 微孔容量

* 饱和容量

这些概念更接近物理现实，因此更适用于可靠的解释与实际应用。

比表面积及孔径推荐设备国仪量子比表面及孔径分析仪Sicope40 介绍：

参考文献：

"Characterization of Porous Solids VII",Studies in Surface Science and Catalysis, Vol 160, P.Llewellyn, F.Rodriguez-Reinoso, J.Rouquerol and N.Seaton Eds.(2007), Elsevier, Amsterdam and Oxford, pp49-56